Pada artikel ini kita akan melatih dan memperdalam pengetahuan kita mengenai Contoh Soal Cerita SPLDV dengan Pembahasan secara mudah dan jelas
tugassains.com – Sistem Persamaan Linear Dua Variabel SPLDV merupakan salah satu persamaan linear yang memiliki dua buah variabel dimana masing masing variabel memiliki penyelesaian yang pasti.
Untuk menyelesaikan spldv terdapat banyak cara untuk dapat menyelesaikannya yaitu:
- SPLDV Metode Subtitusi
- SPLDV Metode Eliminasi dan
- SPLDV Metode Grafik. Yang mana meskipun terdapat banyak cara untuk menyelesaikan persamaan, nilai variabel akan memiliki nilai yang tetap.
Berikut adalah contoh soal cerita spldv yang dapat dijadikan bahan pembelajaran.
Contoh Soal Cerita SPLDV
1. Rudi membeli 2 kg anggur dan 1 kg jeruk dan ia harus membayar Rp15.000,00, sedangkan Rizki membeli 1 kg anggur dan 2 kg jeruk dengan harga Rp18.000,00. Berapakah harga 5 kg anggur dan 3 kg jeruk?
Jawab: Untuk menyelesaikan soal cerita sistem persamaan linear dua variabel langkah pertama yaitu dengan memisalkan variabelnya:
Misal:
anggur = x, jeruk = y
Rudi → 2x + y =
15.000 …..(1)
Rizki → x + 2y = 18.000 …..(2) (jika hanya satu koefisien tuliskan variabel saja 1x = x)
Ditanya: 5x + 3y =?
Kemudian kita akan menyelesaikan persamaan linear dua variabel tersebut dengan mengeliminasi y dari persamaan untuk mengetahui nilai x atau harga anggur:

Kemudian kita substitusi nilai x = 4000 ke persamaan 1 untuk mencari nilai y atau harga jeruk:
2x + y = 15.000
2(4.000) + y = 15.000
8.000 + y =15.000
y = 15.000 – 8.000
y = 7.000
Jadi harga anggur atau x Rp. 4.000/kg dan jeruk atau y Rp. 7.000/kg, selanjutnya adalah menjawab besar harga 5 kg anggur dan 3 kg jeruk.
5x + 3y = 5(4.000) + 3(7.000) = 20.000 +21.000 = 41.000
Jadi harga 5 kg anggur dan 3 kg jeruk Rp. 41.000
2. Sebuah toko pakaian menjual kemeja dan celana, didalam daftar harga terdapat harga 1 buah kemeja dan 3 celana seharga Rp. 82.000, sedangkan harga 3 buah kemeja dan 2 celana sebesar Rp. 99.000.
Berapa harga masing-masing kemeja dan celana?

Jawab: Misalkan terlebih dahulu variabel yaitu kemeja dan celana untuk mempermudah perhitungan persamaan linear dua variabel.
Misal:
kemeja = a, celana = b
a + 3b = 82.000 …..(1)
3a + 2b = 99.000 …..(2)
Ditanya: harga masing-masing kemeja dan celana? (nilai a dan b)
Untuk mengetahui harga masing-masing kemeja dan celana kita dapat menggunakan metode campuran yaitu metode eliminasi dengan metode substitusi. Lakukan eliminasi nilai a untuk mengetahui nilai b dari persamaan.
Kemudian sustitusi nilai b = 21.000 ke persamaan satu untuk mencari nilai a.
a + 3b = 82.000
a + 3(21.000) = 82.000
a + 63.000 = 82.000
a = 82.000 – 63.000
a = 19.000
Jadi harga kemeja atau a sebesar Rp. 19.000 dan harga celana atau b sebesar Rp. 21.000.
3. Diketahui di suatu keluarga berat badan ayah sama dengan berat badan anak ditambah 46kg, dan jumlah berat badan ayah dengan anak sebesar 68kg. Tentukan berat ayah dan anak tersebut.
Jawab: Untuk menyelesaikan soal dari permasalahan tersebut mari kita buat dalam bentuk persamaan linear dua variabel terlebih dahulu
Misal:
Berat Badan Ayah = x dan Berat Badan Anak = y.
x = y + 50 ……(1)
x + y = 94 ……(2)
Ditanya:Umur ayah dan anak x =? dan y=?
Untuk menyelesaikan soal ini kita dapat dengan mudah menggunakan Metode Substitusi dengan mensubstitusikan persamaan satu ke dalam persamaan 2 untuk mencari nilai y.
x + y = 94
(y + 50) + y = 94 →
substitusi persamaan 1, x = y + 50.
y + y + 50 = 94
2y = 94 – 50
y = 44/2
y = 22
Setelah mengetahui berat badan anak atau y substitusikan nilai y = 22 ke dalam persamaan 1 untuk mengetahui berat badan ayah.
x = y + 50
x = 22 + 50
x = 72
Sehingga kita memperoleh berat badan ayah = 72kg dan berat badan anak 22kg.
4. Harga 3kg Anggur dan 5kg Apel adalah Rp. 160.000, sedangkan harga 4kg Anggur dan 1kg Apel adalah Rp. 134.000. Jika Zaki membeli 2kg Anggur dan 2kg Apel dengan membawa uang Rp. 100.000 maka besar uang kembaliannya adalah?
Jawab: Misalkan terlebih dahulu persamaan tersebut dalam bentuk persamaan linear dua variabel agar mudah dalam perhitungan.
Misal:
Anggur = a dan Apel = b
3a + 5b = 160.000 …(1)
4a + b = 134.000 …(2)
Pembelian Zaki = 2a + 2b
ditanya: Kembalian uang Zaki (Kembalian = 100.000 – (2a + 2b))?
Penyelesaian: Untuk menyelesaikan persamaan linear dua variabel tersebut kita dapat melakukan metode eliminasi.
Eliminasi a dari persamaan 1 dan 2 untuk mencari nilai b:
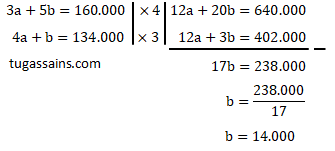
Diperoleh nilai b = 14.000, selanjutnya subtitusi nilai b = 14.000 ke persamaan 1 untuk mencari nilai a.
3a + 5b = 160.000
3a + 5(14.000) = 160.000
3a + 70.000 = 160.000
3a = 160.000 -70.000
a = 90.000/3
a = 30.000
Sehingga diperoleh nilai a = 30.000 dan b = 14.000, Cari nilai 2a + 2b untuk dapat menentukan uang kembalian dari Zaki.
2a + 2b = 2(30.000) + 2(14.000)
2a + 2b = 60.000 + 28.000
2a + 2b = 88.000
Hitung besar kembalian uang Zaki saat membeli 2kg Anggur dan 2kg Apel.
Kembalian = 100.000 – (2a + 2b)
Kembalian = 100.000 – 88.000
Kembalian = 12.000
Jadi uang kembalian Zaki sebesar Rp. 12.000 .
5. Ibu Siti membeli 2 kg tomat dan 3 kg ubi jalar dengan harga Rp. 42.000 di pasar dengan Ibu Sri membeli 5 kg tomat dan 1 kg ubi jalar dengan harga Rp. 46.500 . Tentukan harga tomat dan ubi jalar perkg di pasar tersebut!
Penyelesaian: misalkan tomat adalah x dan ubi jalar adalah y
2x + 3y = 42.000 …(1)
5x + y = 46.500 …(2)
Kita dapat mencari nilai x dan y atau harga tomat dan ubi jalar per kg dengan menggunakan metode subtitusi untuk menyelesaikan spldv tersebut. Yaitu pada persamaan 2 dapat diubah dalam bentuk y =
5x + y = 46.500
y = 46.500 – 5x …(3)
Selanjutnya subtitusi persamaan 3 ke persamaan 1 untuk mencari nilai x.
2x + 3y = 42.000
2x + 3(46.500 – 5x) = 42.000
2x + 139.500
-15x = 42.000
-13x = 42.000 – 139.500
-13x = -97.500
x = -97.500/-13
x = 7.500
Sehingga nilai x atau harga tomat per kg adalah Rp. 7.500 selanjutnya cari nilai y atau harga ubi jalar per kg dengan subtiusi nilai x ke persamaan 1.
2x + 3y = 42.000
2(7.500) + 3y = 42.000
15.000 + 3y = 42.000
3y = 27.000
y = 27.000/3
y = 9.000
Jadi nilai y atau harga ubi jalar per kg adalah Rp. 9.000.
Baca Juga: Cara Cepat Menyelesaikan SPLDV
Sekian terima kasih semoga bermanfaat dan jangan lupa bagikan, jika ada yang mau di tanya kan silahkan di kolom komentar.




