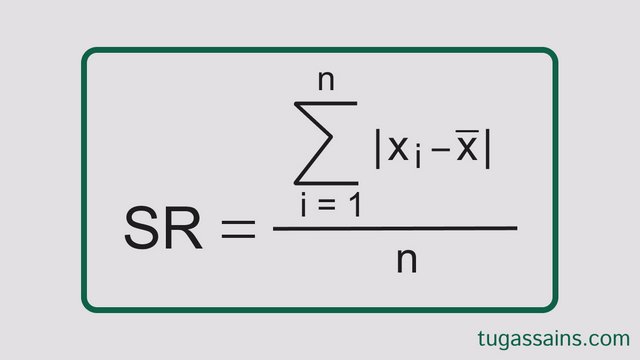 |
| Simpangan Rata-rata |
tugassains.com – Simpangan rata-rata atau Mean deviasi merupakan suatu
metode perhitungan terhadap
Data Tunggal dan Data Berkelompok
dalam menganalisa penyebaran data statistika.
Pengertian Simpangan Rata-rata
Simpangan Rata-rata (Mean Deviation) adalah jumlah harga mutlak selisih setiap
nilai (xi) dengan nilai rata-rata (x̄) dibagi dengan banyak data (n).
Dalam Matematika dinotasikan sebagai singkatan SR atau MD.
Kegunaan dari menghitung Mean Deviasi tersebut adalah untuk mengetahui
seberapa jauh nilai keseluruhan data menyimpang dari nilai rata-rata data
statistika.
Baca juga Rumus dan Cara Menghitung Rata-rata Statistika
Rumus Simpangan Rata-rata
Rumus Simpangan Rata-rata Data Tunggal
Dalam data tunggal dapat kita hitung dengan membagi
jumlah selisih nilai data dengan nilai rata-rata terhadap nilai data:
 |
| Rumus Simpangan Rata-rata Data Tunggal |
Keterangan:
SR = Simpangan Rata-rata
xi = nilai data ke-i
x̄
= nilai rata-rata dari data berkelompok
n = banyak data
Rumus Simpangan Rata-rata Data Kelompok
Dalam data berkelompok dapat dihitung dengan membagikan total dari
perkalian selisih antara rata-rata dan nilai tengah dengan frekuensi terhadap
banyak jumlah seluruh frekuensi data seperti berikut:
 |
| Rumus Simpangan Rata-rata Data Kelompok |
Keterangan:
SR = Simpangan Rata-rata
fi =
besar frekuensi data kelas ke-i
xi = nilai tengah data
kelas ke-i
x̄ = nilai rata-rata dari data berkelompok
Contoh Soal Simpangan Rata-rata
Berikut ini adalah contoh soal yang disertai dengan pembahasan untuk
melengkapi materi, sebagai bahan pembelajaran.
Pada Data Tunggal
1. Diketahui nilai ujian matematika mahasiswa disuatu kelas yaitu 7, 8,
6, 8, 10, 8, 9. Dari data tunggal nilai ujian tersebut carilah nilai simpangan
rata-rata!
Jawab:
Hitung nilai mean/rata data tunggal terlebih dahulu:
Kemudian hitung nilai dengan menggunakan rumus SR data tunggal seperti
berikut:
Jadi nilai simpangan rata-rata dari nilai mahasiswa tersebut sebesar 6/7.
2. Dari sebuah data tunggal 4, 6, 12, 16, 22 Carilah besar nilai mean
deviasi dari data tunggal tersebut!
Jawab:
Dari data tunggal tersebut hitung terlebih dahulu nilai mean data tunggal:
Setelah mengetahui nilai rata-rata dari data tunggal tersebut, selanjutnya
kita hitung nilai mean deviasi sesuai dengan rumus.
Jadi nilai mean deviasi dari data tunggal tersebut sebesar 5,6.
3. Hitunglah nilai mean deviasi dari data 6, 8, 7, 4, 5.
Jawab:
Hitung terlebih dahulu nilai mean dari data tunggal tersebut.
Setelah itu hitung mean deviasi dari data tersebut
Jadi besar nilai mean deviasi dari data tersebut sebesar 1,2.
Pada Data Kelompok
1. Di sebuah perusahaan produsen teknologi sedang melakukan survei terkait kinerja perusahaan kepada pada para pelanggannya, kemudian dilakukan pendataan mengenai sebaran umur partisipan survei dalam bentuk histogram sebagai berikut.
 |
| Contoh Soal Simpangan Rata-rata Data Kelompok |
Dari data sebaran umur partisipan survei tersebut carilah nilai simpangan rata-ratanya!
penyelesaian:
Sesuai dengan rumus kita akan mencari nilai rata-rata data kelompok terlebih dahulu, hitung dengan bantuan tabel.
Nilai titik tengah diperoleh dari:
titik tengah (xi) = (batas atas + batas atas)/2
Diperoleh nilai rata-rata data:
x̄ = Σfixi / Σfi
= 1.300/40
= 32,5
Selanjutnya hitung nilai simpangan rata-rata dengan bantuan tabel kembali.
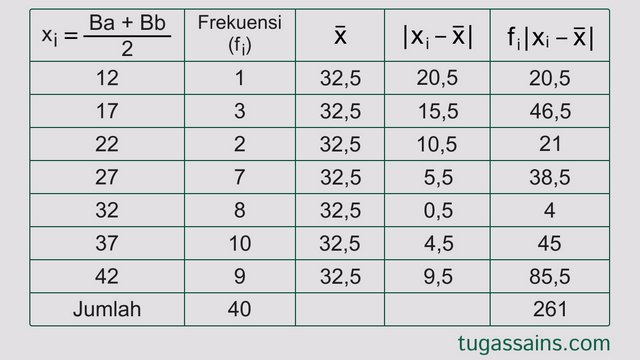
Sehingga diperoleh hasil perhitungan:
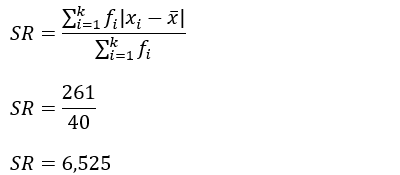
Jadi nilai simpangan rata-rata dari data sebaran umur tersebut sebesar 6,525.
2. Dari tabel distribusi frekuensi berat badan pegawai disuatu kantor marketing berikut, hitunglah nilai simpangan rata-ratanya!
penyelesaian:
Cari terlebih dahulu besar rata-rata dari data tersebut dengan membagikan
hasil perkalian antara titik tengah dengan frekuensi terhadap jumlah
frekuensi.
Selanjutnya cari besar mean deviasi menggunakan tabel bantu agar lebih mudah
dalam perhitungan:
Jadi besar mean deviasi dari data tersebut sebesar 7,4.
Baca juga
Pengertian, Rumus dan Contoh Soal Ragam Varians
Terima kasih semoga bermanfaat dan jangan lupa bagikan, jika ada yang ingin
ditanyakan silahkan tanya dikolom komentar.